힙 정렬(heap sort)에 대해 알아보자

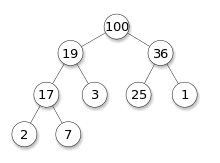
트리를 구성해 정렬을 하는 힙 정렬에 대해 알아보자

힙(heap)
힙 정렬 과정
힙 정렬 구현
힙 정렬 특징
힙 정렬 시간복잡도

힙 정렬(heap sort) 알고리즘

최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법
내림차순 정렬 : 최대 힙, 오름차순 정렬 : 최소 힙 구성

힙(heap)

최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 자료구조.
위 그림은 최대 힙으로 모든 부모 노드가 자식 노드보다 큰 값을 갖는다.

자료구조 ‘힙(heap)‘에 대해서는 이후 새로운 글에서 자세히 다루겠다.

힙 정렬 과정

주어진 원소들로 최대 힙을 구성
최대 힙의 루트 노드(==현재 배열의 첫 번째 요소 == 최댓값)와 말단 노드(==현재 배열의 마지막 요소)를 교환
새 루트 노드에 대해 최대 힙을 구성
원소의 개수 만큼 2와 3을 반복

이 때, 주어진 자료 구조에서 힙 성질을 만족하도록 하는 연산을 heapify라고 한다.(3번 과정)

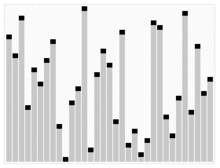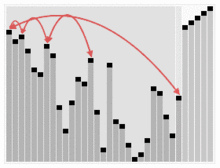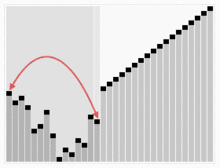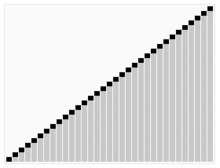
Sorting heapsort anim.gif

힙 정렬 구현 (python)

def heapify(arr, index, heap_size):
    # 완전이진트리는 배열 하나로 트리 구현가능
    largest = index
    left = index * 2 + 1    # 왼쪽 자식
    right = index * 2 + 2   # 오른쪽 자식
    # 왼쪽 자식이 현재 요소보다 크면 인덱스 교체
    if left < heap_size and arr[left] > arr[largest]:
        largest = left
    # 오른쪽 자식이 현재 요소보다 크면 인덱스 교체
    if right < heap_size and arr[right] > arr[largest]:
        largest = right
    # 교체된적이 있다면 교체된 index와 largest 요소값 교체
    if largest != index:
        arr[largest], arr[index] = arr[index], arr[largest]
        # 변경되었으면 변경된 부분을 중심으로 다시 한번 heapify
        heapify(arr, largest, heap_size)


def heap_sort(arr):
    n = len(arr)

    # 최초 힙
    # 트리의 절반부터 거꾸로 올라가며 heapify를 하는것이 효율적
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, i, n)

    # 한번 구성된 힙을 정렬.
    # 가장 큰 값(루트) 를 가장 끝 값으로 이동한 후 힙 생성.
    for i in range(n - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        heapify(arr, 0, i)
    return arr


data = [61, 324, 21, 56, 243, 6, 1, 634, 43, 3, 52]
print(heap_sort(data))

힙 정렬 구현 (C)

#include <stdio.h>

void heapify(int *arr, int index, int heap_size) {
	int largest = index;
	int left = index * 2 + 1;
	int right = index * 2 + 2;
	int temp;

	// 왼쪽 자식이 현재 요소보다 크면 인덱스 교체
	if (left < heap_size && arr[left] > arr[largest]) {
		largest = left;
	}
	// 오른쪽 자식이 현재 요소보다 크면 인덱스 교체
	if (right < heap_size && arr[right] > arr[largest]) {
		largest = right;
	}
	// 교체되었다면 index와 largest 요소값 교체
	if (largest != index) {
		temp = arr[largest];
		arr[largest] = arr[index];
		arr[index] = temp;
		// 변경 후 변경된 부분을 중심으로 다시 한 번 heapify
		heapify(arr, largest, heap_size);
	}

}
void heap_sort(int *arr, int heap_size) {
	int temp;
	// 최초 힙
	// 트리의 절반부터 거꾸로 올라가며 heapify
	for (int i = heap_size / 2; i >= 0; i--) {
		heapify(arr, i, heap_size);
	}

	// 한번 구성된 힙을 크기별로 정렬.
	// 가장 큰 값(루트)를 인덱스 맨 뒤로 보낸 뒤 힙 생성
	for (int i = heap_size - 1; i >= 0; i--) {
		temp = arr[0];
		arr[0] = arr[i];
		arr[i] = temp;
		heapify(arr, 0, i);
	}
}

int main(void) {
	int data[20] = { 61, 324, 21, 56, 243, 6, 1, 634, 43, 3, 52 };
	int n = 11;
	heap_sort(data, n);
	for (int i = 0; i < n; i++) printf("%d ", data[i]);

	return 0;
}