책 정리와 같은 방식으로 정리하는 삽입 정렬에 대해 알아보자.
삽입 정렬(insertion sort) 알고리즘
-
책을 순서대로 정렬하는 방법과 유사.
- 정렬되어 있는 책 사이의 올바른 자리를 찾아 삽입한다.
- 새로 삽입될 카드의 수만큼 반복. 전체 카드가 정렬된다.
- 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘.
- k번째 반복 후의 결과 배열은, 앞쪽 k + 1 항목이 정렬된 상태
삽입 정렬 과정
- k번째 요소가 이미 정렬된 배열에서의 알맞은 자리를 찾는다.
- 알맞은 자리부터 k-1번째 요소까지 한칸씩 뒤로 민 후 알맞은 자리에 k 번째 요소를 삽입한다.
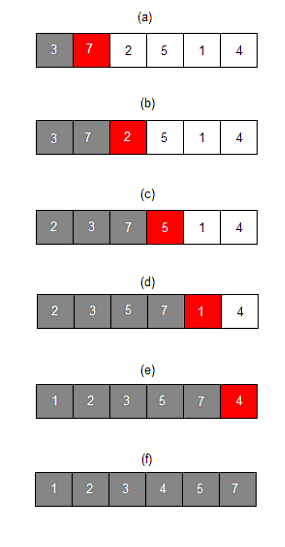
각 반복에서 정렬되지 않은 나머지 부분 중 첫 번째 항목은 제거되어 정확한 위치에 삽입된다. 그러므로 다음과 같은 결과가 된다.
a. 정렬된 3과 현재 7을 비교. 변경 x
b. 정렬된 3, 7과 현재 2를 비교. 3 앞으로 삽입
c. 정렬된 2, 3, 7과 현재 5를 비교. 3과 7 사이로 삽입.
d. 정렬된 2, 3, 5, 7과 현재 1을 비교. 2 앞으로 삽입
e. 정렬된 1, 2, 3, 5, 7과 현재 4를 비교. 3과 5 사이로 삽입.
f. 정렬된 1, 2, 3, 4, 5, 7
삽입 정렬 구현 (python)
def insertion_sort(data):
for i in range(1, len(data)): # 현재 바꿀 index == i
j = i-1 # 바꿀 인덱스보다 한 칸 앞
key = data[i] # 바꿀 인덱스의 요소값
while data[j] > key and j >= 0:
# 이미 정렬된 인덱스가 현재 값보다 크고, 가리키는 인덱스가 0보다 크거나 같을때
data[j+1] = data[j] # 계속해서 data는 한칸씩 뒤로 밀린다.
j -= 1 # 인덱스 값을 하나씩 앞으로 당긴다.
data[j+1] = key # while문 탈출시 빈 칸에 key값 넣기
data = [3, 5, 2, 6, 7, 1, 4]
insertion_sort(data)
print(data)삽입 정렬 구현 (C)
#include <stdio.h>
void insertion_sort(int arr[], int n) {
int i, j, key;
for (i = 1; i < n; i++) {
key = arr[i];
for (j = i - 1; j >= 0 && arr[j] > key; j--) {
arr[j + 1] = arr[j];
}
arr[j + 1] = key;
}
}
int main(void) {
int data[7] = { 3, 5, 2, 6, 7, 1, 4 };
int n = 7;
insertion_sort(data, n);
for (int i = 0; i < n; i++) {
printf("%d ", data[i]);
}
return 0;
}삽입 정렬의 특징
-
장점
- 시간복잡도가 O(n^2)이나 다른 O(n^2) 알고리즘(선택정렬, 버블정렬) 보다는 빠르다.
- 안정 정렬이다.
- in-place 알고리즘이다.
- 구현이 간단하다.
- 대부분 이미 정렬되어 있는 경우에 매우 효율적이다.
-
단점
- 배열의 크기가 클 경우에 적합하지 않다.
- 비교적 많은 이동을 포함한다.
삽입 정렬의 시간복잡도
- O(n^2) => 2중 for문
-
최선의 경우
- 비교
- 외부 루프 n-1번
- 교환 없음
- T(n) = O(n)
-
최악의 경우
- 비교
- 1 + 2 + 3 + … + n-2 + n-1 = n(n-1) / 2번
- 교환
- 각 단계마다 i+2번 이동
- T(n) = O(n^2)