분할 정복 중 하나인 합병 정렬에 대해 알아보자
합병 정렬(merge sort) 알고리즘
- 분할 정복 알고리즘의 하나
-
병합해놓은 리스트를 원본에 복사하는 과정 등이 필요하기 때문에 시간이 오래 걸린다.
- linked list로 사용하게 되면 효율이 좋아진다.
합병 정렬 과정
-
리스트의 길이가 1 이하면 이미 정렬된 것으로 본다. 그렇지 않을 경우에
- 분할 : 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 만든다.
- 정복 : 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 결합 : 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. 이 때 정렬 결과가 임시 배열에 저장된다.
- 복사 : 임시 배열에 저장된 결과를 원래 배열에 복사한다.
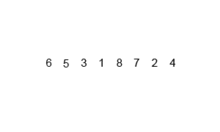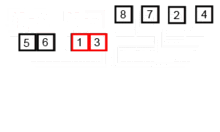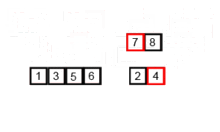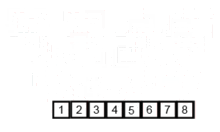
합병 정렬 구현 (python)
def merge_sort(arr):
if len(arr) <= 1:
return arr
# 1. divide
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 리스트의 길이가 1이 될 때 까지 divide
left = merge_sort(left)
right = merge_sort(right)
# merge 부분
return merge(left, right)
def merge(left, right):
# 복사할 임시 배열
result = []
# 양쪽 두 리스트 중 하나라도 원소가 없을 때 까지 반복
while left and right:
if left[0] < right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 만약 왼쪽 혹은 오른쪽 리스트가 남았을 때
# 모두 다 집어넣기
if left:
result.extend(left)
elif right:
result.extend(right)
return result
data = [61, 324, 21, 56, 243, 6, 1, 634, 43, 3, 52]
print(merge_sort(data))합병 정렬 구현 (C)
#include <stdio.h>
void merge(int *arr, int left, int mid, int right) {
int temp[20];
int i = left, j = mid + 1, k = left;
// left의 시작인 i가 mid보다 작거나 같고,
// mid의 시작인 j가 right보다 작거나 같을때까지
while (i <= mid && j <= right) {
// 왼쪽 값이 오른쪽 값보다 작거나 같은 경우 temp 배열에 복사
if (arr[i] <= arr[j]) temp[k++] = arr[i++];
// 반대의 경우에 temp에 복사
else if (arr[i] > arr[j]) temp[k++] = arr[j++];
}
// i가 mid보다 커질 경우(왼쪽 값 모두 복사)
if (i > mid) {
// 오른쪽 값 모두 복사
while (j <= right) temp[k++] = arr[j++];
}
else {
// 반대의 경우 왼쪽 값 모두 복사
while (i <= mid) temp[k++] = arr[i++];
}
// 임시 배열의 값을 원래 배열에 복사
for (int m = left; m <= right; m++) arr[m] = temp[m];
}
void merge_sort(int *arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
// left가 right보다 크거나 같아질 때 까지 반복
merge_sort(arr, left, mid);
merge_sort(arr, mid + 1, right);
// 길이가 비슷해지면 merge
merge(arr, left, mid, right);
}
}
int main(void) {
int data[20] = { 61, 324, 21, 56, 243, 6, 1, 634, 43, 3, 52 };
int n = 11;
merge_sort(data, 0, n-1);
for (int i = 0; i < n; i++) printf("%d ", data[i]);
return 0;
}합병 정렬의 특징
-
장점
- 안정적인 정렬.
- 데이터 분포에 따른 시간 영향을 덜받는다. 똑같은 크기로 나누어 정렬되기 때문에 시간은 동일하다.
- 만약 배열을 linked list(연결 리스트)로 구현하면 인덱스만 변경되므로 데이터의 이동 및 복사를 하지 않아도 된다.
- 크기가 큰 배열을 정렬할 경우 연결리스트를 사용한다면, 합병정렬은 어떤 정렬보다도 효율적이다.
-
단점
- 배열로 구성되어 있을 때, 임시 배열이 필요하다.
- 크기가 큰 경우 많은 이동횟수가 필요하기 때문에 시간 낭비가 될 수 있다.
합병 정렬의 시간복잡도
-
분할
- 단순 분할만 한다. 비교, 이동이 수행되지 않는다.
-
합병
- 비교 : 각 층마다 n번씩 비교
- 순환 호출 : 절반씩 나누어 호출되기 때문에 log n
- 이동 : 임시 배열에 복사했다가 다시 원 배열에 가져와야 하기 때문에 배열의 요소가 n개일 경우, 이동은 2n번 발생.
- T(n) = O(n log n)