분할 정복 중 하나이며, 일반적으로 가장 빠른 퀵 정렬에 대해 알아보자
퀵 정렬(quick sort) 알고리즘
- 비교 정렬이다. 다른 원소와의 비교만으로 정렬을 수행한다.
- 불안정 정렬이다. 같은 값이 있을 경우 같은 값들의 순서를 보장하지 못한다.
- 주어진 배열을 두 개로 분할하고, 각각을 정렬한다. == 분할 정복 알고리즘
-
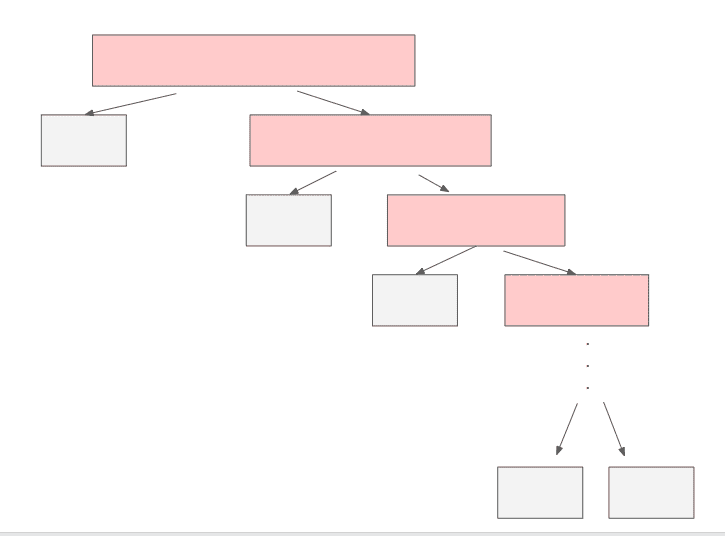
분할 정복(divide and conquer)
- 문제를 작은 2개의 문제로 분리하고 각각을 해결하는 전략.
- 일반적으로 순환 호출을 이용한다.
-
합병정렬과 달리 비균등 분할이다
- 최악의 경우 O(n^2)의 시간복잡도를 갖는다.
- 일반적으로 O(n long n)의 시간 복잡도를 갖는다.
-
아이디어
- 피봇(P) 값들보다 큰 값은 오른쪽, 작은 값들은 왼쪽에 위치시켜서 피봇을 두 집합의 가운데에 위치시킨다.
- 일반적으로, 피봇을 선택할 때 맨 왼쪽 값을 사용하나, 값의 치우침을 방지하기 위해서는
왼쪽 끝오른쪽 끝임의의 값세 개 중 하나를 사용하거나, 중간값을 사용할 수도 있다.
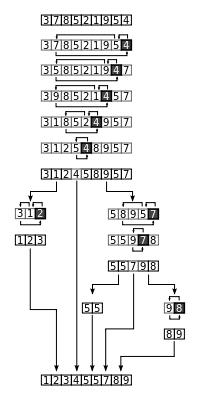
퀵 정렬 과정
- 리스트 가운데 하나의 원소를 고른다. 이렇게 고른 원소를 피봇이라 한다. 일반적으로 정렬되지 않은 맨 왼쪽 값을 선택한다.
- 피봇 앞에는 피봇보다 값이 작은 모든 원소들이 오고, 피봇 뒤에는 피봇보다 값이 큰 모든 원소들이 오도록 피봇 기준으로 리스트를 둘로 분할한다.
- 분할된 두 개의 작은 리스트에 대해 리스트의 크기가 0이나 1이 될 때 까지 재귀적으로 과정을 반복한다.
위는 퀵소트의 그림이다. 피봇 4를 두고 큰 값과 작은 값을 분할하고, 분할된 리스트들을 가지고 반복한다.
퀵 정렬 구현 (python)
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
# pivot = arr[0] 도 무관함.
low = [] # 피봇보다 작음
high = [] # 피봇보다 큼
equal = [] # 피봇이랑 같음. 정렬됨
for i in arr:
if i < pivot:
low.append(i)
elif i > pivot:
high.append(i)
else:
equal.append(i)
# 정렬되지 않은 low와 high를 다시 quick sort
return quick_sort(low) + equal + quick_sort(high)
data = [3, 7, 8, 5, 2, 1, 9, 5, 4]
print(quick_sort(data))위의 방법은 리스트를 매번 만들기 때문에 메모리 사용량이 크다.
퀵 정렬 구현 (C)
#include <stdio.h>
void quick_sort(int *data, int l, int r) {
int L = l, R = r;
if (L > R) return;
int mid = (L + R) / 2;
int pivot = data[mid];
while (L <= R) {
while (data[L] < pivot) L++;
while (pivot < data[R]) R--;
if (L <= R) {
int temp;
temp = data[L];
data[L] = data[R];
data[R] = temp;
L++;
R--;
}
}
if (L < r) quick_sort(data, L, r);
if (l < R) quick_sort(data, l, R);
}
int main(void) {
int data[9] = { 3, 7, 8, 5, 2, 1, 9, 5, 4 };
int l = 0;
int r = 9;
quick_sort(data, 0, r-1);
for (int i = 0; i < r; i++) {
printf("%d ", data[i]);
}
return 0;
}퀵 정렬의 특징
-
장점
- 속도가 빠르다. 시간복잡도를 O(n log n)으로 갖는 다른 알고리즘 보다도 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다. (python처럼 코드 짰을 때 제외)
- O(log n) 만큼의 메모리를 필요로 한다.
-
단점
- 정렬된 리스트에 대해서는 퀵정렬의 불균형 분할에 의해 수행시간이 더 많이 걸린다.
-
단점을 극복하기 위해 피봇을 선택할 때 리스트를 균등하게 분할할 수 있는 데이터를 선택한다.
- 랜덤값, 크기순 중간값 등
퀵 정렬의 시간복잡도
-
최선의 경우
- 비교 : 각 층마다 n번
- 순환 호출 횟수 : log n
- T(n) = O(n log n)
-
최악의 경우
- 일반적으로 알고리즘 문제에서는 정렬되지 않은 값을 주기 때문에 평균적인 경우를 생각한다.
- T(n) = O(n log n)