이진 트리의 거의 모든 순회에 대하여
들어가기 전에
최근 공부를 하다가 “트리를 전위 순회 했을 결과”를 맞추는 문제를 내가 못 풀고 있더라… 아무리 잠시 쉬었다고 해도 내 자신에게 충격을 받아 기억하기 위해 글을 작성한다.
트리 순회(Tree traversal)
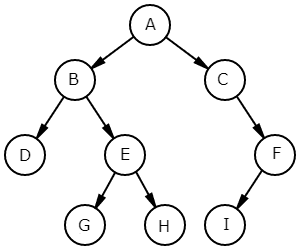
트리 순회란 트리 구조에서 각 노드를 모두 방문하는 것을 말한다. 조금 더 구체적으로 말하면 트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 말한다.
트리의 순회를 말하면 대표적으로 전위 순회, 중위 순회, 후위 순회 3가지를 말할 수 있다. 이후에 레벨 순회라는 순회에 대해서도 포스팅을 해보려고 한다.
사실, 트리 순회를 코드로 작성하는 것은 쉬운 편이다. 트리만 잘 만들어 놓았다면 재귀를 어떻게 사용할 것인가만 잘 선택해주면 된다.
어디를 먼저 방문할 것인지, 현재 노드를 언제 선택할 것인지에 따라 재귀 호출의 위치가 달라진다.
전위 순회(preorder)
트리의 전위 순회는 현재노드 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리 순으로 순회하는 방식이다.
코드 역시 현재 노드를 출력한 후, 왼쪽, 오른쪽 순서대로 함수를 호출한다.
순회 순서 : A -> B ->D -> E -> G -> H ->C -> F -> I
python
def preorder(node):
if node:
print(tree[node][1], end=" ")
preorder(tree[node][2])
preorder(tree[node][3])중위 순회(inorder)
트리의 전위 순회는 왼쪽 서브 트리 -> 현재노드 -> 오른쪽 서브 트리 순으로 순회하는 방식이다.
코드는 왼쪽 함수 호출, 현재 노드 출력, 오른쪽 함수 호출 순서로 진행된다.
순회 순서 : D -> B -> G -> E -> H -> A -> C -> I -> F
python
def inorder(node):
if node:
inorder(tree[node][2])
print(tree[node][1], end=" ")
inorder(tree[node][3])후위 순회(postorder)
트리의 전위 순회는 왼쪽 서브 트리 -> 오른쪽 서브 트리 ->현재노드 순으로 순회하는 방식이다.
후위 순회 또한 왼쪽 함수 호출, 오른쪽 함수 호출, 현재 노드 출력 순서로 진행된다.
순회 순서 : D -> G -> H -> E -> B -> I -> F -> C -> A
python
def postorder(node):
if node:
postorder(tree[node][2])
postorder(tree[node][3])
print(tree[node][1], end=" ")정리
트리의 전위 순회, 중위 순회, 후위 순회는 모두 함수의 재귀 호출에 따라서 사용된다. 특히 후위순회와 같은 경우는 괄호가 있는 사칙연산의 계산에 유용하게 사용될 수 있다.
트리를 어떻게 구현했는가에 따라 함수 호출에 사용되는 변수가 달라질 수는 있지만, 기본적으로 함수를 언제 호출하는가, 언제 출력 하는가에 따라 결과값이 달라진다.
input.txt
9
1 A 2 3
2 B 4 5
3 C 0 6
4 D
5 E 7 8
6 F 9
7 G
8 H
9 Itree_traversal.py
def preorder(node):
if node:
print(tree[node][1], end=" ")
preorder(tree[node][2])
preorder(tree[node][3])
def inorder(node):
if node:
inorder(tree[node][2])
print(tree[node][1], end=" ")
inorder(tree[node][3])
def postorder(node):
if node:
postorder(tree[node][2])
postorder(tree[node][3])
print(tree[node][1], end=" ")
n = int(input())
tree = [[0, 0, 0, 0]]
for i in range(n):
data = list(input().split())
temp = [0, 0, 0, 0]
temp[0] = int(data[0])
temp[1] = data[1]
if len(data) == 3:
temp[2] = int(data[2])
elif len(data) == 4:
temp[2] = int(data[2])
temp[3] = int(data[3])
tree.append(temp)
preorder(1)
print(" -> 전위 순회")
inorder(1)
print(" -> 중위 순회")
postorder(1)
print(" -> 후위 순회")output
A B D E G H C F I -> 전위 순회
D B G E H A C I F -> 중위 순회
D G H E B I F C A -> 후위 순회